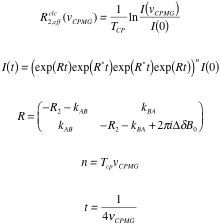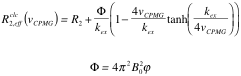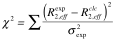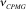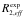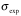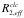In this section, the user can select a model for fitting the data based on a chosen exchange regime.
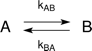
The fittings presume the following kinetic scheme:
The following formulas are used to calculate R2,eff for different models such as the Bloch-McConnell [1], Carver-Richards [2, 3] and Luz-Meiboom [4] models:
| Bloch-McConnell model |
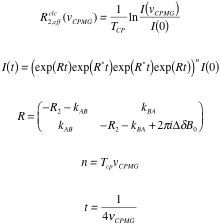 |
| Carver-Richards model |
 |
| Luz-Meiboom model |
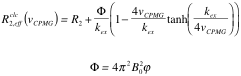 |
| where |
| TCP | given constant relaxation delay |
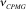 | given CPMG frequency |
| B0 | given field strength for the nuclei of the interest in MHz |
| |
| R2 | fitted intrinsic transverse relaxation rate |
| kAB, kBA | fitted kinetic rate constants (slow exchange) |
| kex | fitted kinetic rate constant (fast exchange) |
| Δδ | fitted chemical shift difference in ppm (slow exchange) |
| φ | fitted population weighted chemical shift difference in ppm2 (fast exchange) |
|
The optimization of the parameters is performed by minimizing the target function:
| where |
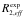 | given experimental relaxation rate |
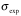 | given experimental error in the relaxation rate |
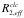 | calculated relaxation rate based on model |
|
References
| [1] | McConnell, H. M. (1958) Reaction rates by nuclear magnetic resonance, J. Chem. Phys. 28, 430- 431 |
| [2] | Davis, D.G. et al. (1994) Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1 rho and T2 (CPMG) methods. J. Magn. Reson. B, 104, 266–275. |
| [3] | Carver, J. P.; Richards, R. E. (1972) General 2-site solution for chemical exchange produced dependence of T2 upon Carr-Purcell pulse separation J. Magn. Reson., 6, 89-96. |
| [4] | Luz, Z. and Meiboom, S. (1963) Nuclear Magnetic Resonance study of the protolysis of trimethylammonium ion in aqueous solution—order of the reaction with respect to solvent. J. Chem. Phys., 39, 366–370. |