Help
File upload
Define your experimental data in this section. More then one file can be uploaded, each file representing data measured at different magnetic field. If data were measured at multiple field strengths, the residue types and numbers will be compared and chemical shift differences fitted globally to calculate kinetic parameters.
The input-file should have the following format:
| 1st line | Value of the B0 field for the nuclei of interest in MHz (e.g. 60.12). |
| 2nd line | Value of the constant relaxation time for the CPMG experiment in seconds (e.g. 0.04). |
| 3rd line | Comment line. In the example file, we described the data format (e.g. #nu_cpmg(Hz) R2(1/s) Esd(R2)). |
| > 3rd line |
The first line of the block defines the residue type and number and optionally the intrinsic relaxation rate R20 from HEROINE experiment. The following lines contain the CPMG frequencies ( 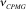 , s-1), relaxation rates ( , s-1), relaxation rates (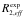 , s-1) and errors in relaxation rates ( , s-1) and errors in relaxation rates (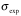 , s-1). , s-1).
|
Example file
CPMG
60.12 0.040000 #nu_cpmg(Hz) R2(1/s) Esd(R2) # A1 50.000 37.060 0.746 100.000 38.590 0.738 200.000 37.794 0.725 300.000 34.686 0.700 400.000 32.837 0.639 500.000 27.971 0.583 600.000 27.488 0.541 700.000 26.366 0.510 800.000 23.926 0.488 900.000 23.141 0.472 1000.000 22.697 0.459 # B2 50.000 32.844 0.656 100.000 32.088 0.639 200.000 30.126 0.593 ...
CPMG+HEROINE
60.12 0.040000 #nu_cpmg(Hz) R2(1/s) Esd(R2) # A1 R2_0: 20.000 50.000 37.060 0.746 100.000 38.590 0.738 200.000 37.794 0.725 300.000 34.686 0.700 400.000 32.837 0.639 500.000 27.971 0.583 600.000 27.488 0.541 700.000 26.366 0.510 800.000 23.926 0.488 900.000 23.141 0.472 1000.000 22.697 0.459 # B2 R2_0: 20.000 50.000 32.844 0.656 100.000 32.088 0.639 200.000 30.126 0.593 ...
Residue selection
In this section, the user selects an appropriate set of residues. ShereKhan's suggestion is based on the calculation of the α-values. If data at several B0 fields are provided, ShereKhan performs the following analysis of the exchange regimes [5]:
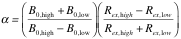
| where |
|
The calculated α-values can be used to estimate the exchange regime:
1 < α ≤ 2 fast exchange
Exchange regime and exchange model
In this section, the user can select a model for fitting the data based on a chosen exchange regime.
The fittings presume the following kinetic scheme:
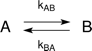
The following formulas are used to calculate R2,eff for different models such as the Bloch-McConnell [1], Carver-Richards [2, 3] and Luz-Meiboom [4] models:
| Bloch-McConnell model | 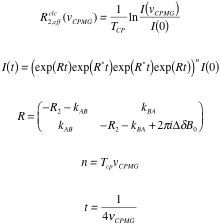 |
| Carver-Richards model |  |
| Luz-Meiboom model | 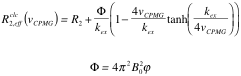 |
| where |
|
The optimization of the parameters is performed by minimizing the target function:
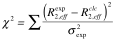
| where |
|
Model parameters
Results
The results of the calculations are presented in this section. The values of globally fitted parameters are:
| Slow exchange | Forward and backward rates kAB and kBA Exchange rate kex = kAB + kBA Population 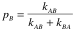
|
| Fast exchange | Exchange rate kex = kAB + kBA |
The chemical shift differences Δδ for the slow exchange regime and population weighted chemical shift differences φ for the fast exchange regime are fitted separately for each residue. Intrinsic relaxation rates are fitted for each residue and each B0 field value.
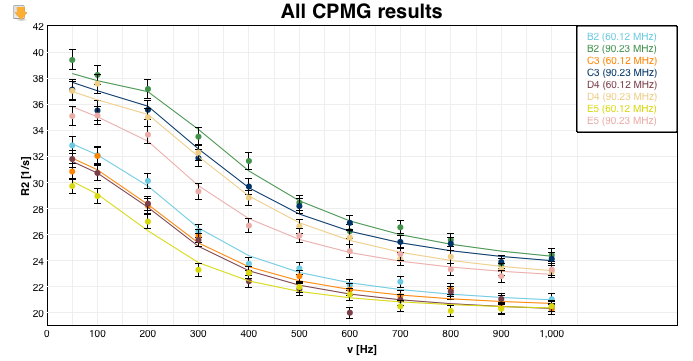
ShereKhan provides a graphical presentation of the experimental and calculated dispersion profiles. Moreover, plots for individual residues are available to check the details of the fitting results. Additional plots either shows chemical shift differences Δδ for the slow exchange regime or φ values for the fast exchange regime. A pdf file with dispersion curves and a summary output file (log file) are available for download.
Graphics
Fitting of the experimental data. The graphs can be downloaded in SVG, PDF, PNG and JPG format. Moving over the residues in the legend (top right corner) will highlight the corresponding data of the respective amino acid at the given field strength.
References
| [1] | McConnell, H. M. (1958) Reaction rates by nuclear magnetic resonance, J. Chem. Phys. 28, 430- 431 |
| [2] | Davis, D.G. et al. (1994) Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1 rho and T2 (CPMG) methods. J. Magn. Reson. B, 104, 266–275. |
| [3] | Carver, J. P.; Richards, R. E. (1972) General 2-site solution for chemical exchange produced dependence of T2 upon Carr-Purcell pulse separation J. Magn. Reson., 6, 89-96. |
| [4] | Luz, Z. and Meiboom, S. (1963) Nuclear Magnetic Resonance study of the protolysis of trimethylammonium ion in aqueous solution—order of the reaction with respect to solvent. J. Chem. Phys., 39, 366–370. |
| [5] | Millet, O. et al. (2000) The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J. Am. Chem. Soc., 122, 2867–2877. |